Олимпиада проводится при поддержке Московского физико-технического института, Компьютерной компании НИКС, Компании Yandex
Информационная поддержка:
журнал "Мир ПК"
IV Открытая олимпиада школьников по программированию, 2009/10 учебный год
Задача J. Авангардная архитектура
| Имя входного файла: | j.in |
| Имя выходного файла: | j.out |
| Максимальное время работы на одном тесте: | 2 секунды |
| Максимальный объем используемой памяти: | 64 мегабайта |
Один из столичных девелоперов решил построить жилой дом по проекту известного авангардного архитектора. Жилой дом будет состоять из квартир-кубиков и иметь причудливую форму. Есть два ограничения, одно из которых наложено архитектором, а второе - законами физики.
Архитектор хочет, чтобы каждый этаж представлял собой связанную последовательность кубиков (разделенные этажи - это мода 1990х). В то же время необходимо, чтобы хотя бы под одним из кубиков этажа находился кубик предыдущего этажа. Первый этаж должен опираться о землю.
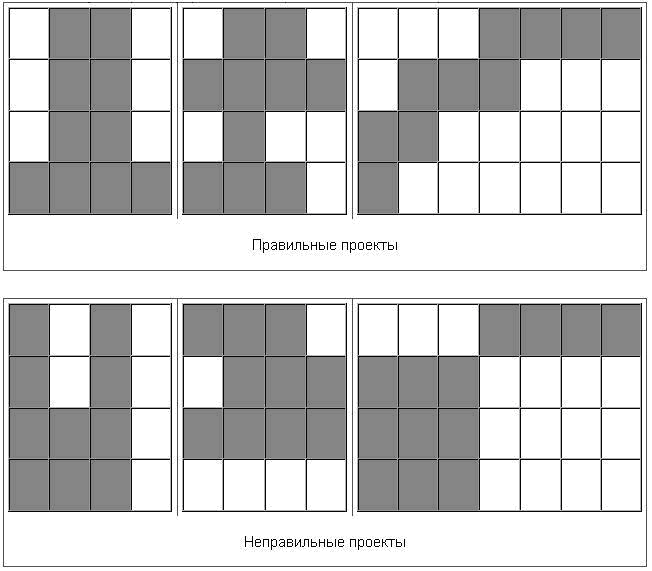
Кроме законов физики архитектора ограничивает также необходимость все это творчество продать. Поскольку покупатели неохотно покупают недвижимость, необходимо привлечь их хоть чем-нибудь, в частности, видом из окна. Специалисты компании-девелопера составили таблицу, в которой для каждого возможного расположения квартиры указана привлекательность вида из окна для этого расположения. Необходимо максимизировать суммарную привлекательность видов из окна.
В приведенном примере показаны привлекательности видов из окна и наилучшее здание из 10 кубиков в данном случае.
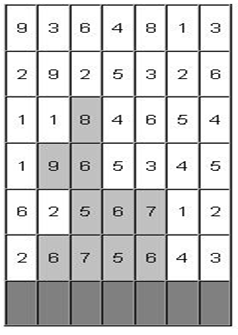
По известному количеству кубиков и таблице привлекательности видов из окна вам необходимо выбрать лучший проект (с максимальной суммарной привлекательностью), удовлетворяющий условиям архитектора и законам физики.
Формат входных данных
В первой строке входного файла указаны натуральные числа N, H и W (1 ≤ H ≤ 30, 1 ≤ W ≤ 30, 1 ≤ N ≤ HW) - количество имеющихся кубиков, максимальная высота и максимальная ширина здания. Следующие H строк содержат по W натуральных чисел, задающих привлекательность соответствующего расположения квартиры. Привлекательность измеряется в пределах от 1 до 100 000 включительно.
Формат выходных данных
Выведите одно число - наибольшую суммарную привлекательность.
Пример
| j.in | j.out |
10 6 7 9 3 6 4 8 1 3 2 9 2 5 3 2 6 1 1 8 4 6 5 4 1 9 6 5 3 4 5 6 2 5 6 7 1 2 2 6 7 5 6 4 3 |
65 |